ご存じの通り、2025度末から経済価値ベースのソルベンシー規制が導入されます。本規制導入の準備に携わっている方々は今更（？）と思うこともあると思いますが、少しお付き合いください。

以下、現行規制の健全性指標のソルベンシー・マージン比率をSMR、経済価値ベースの新規制の健全性指標をESR（Economic Solvency Ratio）と呼びます。

SMRについて、詳細に触れるつもりはありませんが、比較的シンプルに計算できるものと思っています。私も業務で触れたことがありますが、必要なデータが揃ってから数時間〜1日程度でSMRの計算が完了するものと思います。（ディスクロージャー誌や決算状況表などの成果物一式を作成することにはそれなりに時間がかかりますが、ここでは触れないものとします。）

というのも、SMRの計算は、決算業務の成果物に、いくつかの補正を加えて計算できるからです。

アクチュアリー試験の2次試験の生保2の教科書にソルベンシーの章がありますが、他の章よりも分厚く内容も充実しているため、私は試験勉強ではソルベンシーの章に時間を十分に割いてきました。しかし、初めて実務でSMRの計算を行ったときは、試験勉強で感じたほどの労力を感じませんでした。

計算項目は多いと思いますが、計算がシンプルであるため、計算ツール等を整備していれば、労力はそこまでかからないものと思います。

さて、SMRの話が長くなってしまったが、ESRの話に移ります。

内部モデルが充実している会社では、以前から内部モデルでESRの計算をしているかもしれませんが、金融庁のフィールドテストを通じて初めてESRに触れた方も多いと思います。

フィールドテストを担当された多くの方から「非常に大変」という声を聴きます。私も初めて担当した年は、想像以上に大変だった記憶があります。それには、単にESRを計算するだけでなく、感応度分析や変動要因分析、検証レポート等の対応が必要になる点が挙げられますが、ここではSMRとの比較のために、これらの追加的な対応は考えず、ベースのESRの計算のみにフォーカスを置きます。

SMRと比べ、ESRの計算で特徴なのが、将来のキャッシュフローの現価（いわゆるオフバランス項目等）を用いて評価するという点、ストレステストのようなキャッシュフローにショックを与えてリスクを計算するという点などが挙げられますが、上記で述べたようなSMRの計算手法とは全く異なります。

リスクの計算方法について、2022年のアクチュアリー試験の生保2に、リスク計測モデルについて比較している問題があるので参考になると思います。そこでは、SMRがファクターモデル、ESRがショックモデル（ストレステスト）に該当します。

このESRの計算が今年度末から規制導入されることになり、今まではフィールドテストで年1回の計算だったものが少なくとも半期に1度の計算が求められ、今まで以上に大変になることが想定されます。また、ESRが経営指標にも用いられ、中期経営計画等では将来時点のESRの計算も求められるようになると思われます。（実際に、すでにそうしている会社も多いでしょう。）

経営判断においては、「○○という取り組みがESRにどう影響を与えるのか？」と経営陣から問われることがあるでしょう。意思決定のために、様々なパターンのESRの計算が求められるかもしれません。

では、中間管理職からアクチュアリー部門にこのような試算を依頼する場面を想定してみましょう。中間管理職はESRの計算の大変さを把握でいるかもしれないため、「簡便手法でもよいからESRへの影響度を見積もってほしい」と依頼する可能性があります。しかし、アクチュアリー部門は「簡便に見積もれないので時間をかけて精緻に計算します」と答えるかもしれません。中間管理職は「精緻に計算できるなら…、それでお願いします」と。

私も実際にそういう場面に遭遇したことがありますが、非常にもったいないと思っています。もったいないというのは、時間やコスト面だけでなく、専門性の面もです。

ESRの計算は、確かに複雑で、簡便に計算することは難しいと思いますが、アクチュアリーとしてはそれにトライする価値があると思っています。もちろん、開示する指標等については精度やガバナンス上の観点が求められますが、そうでない場合もあるのと思います。

少し関数を使って説明しますが、ESRを関数（写像）で表すと、例えば、

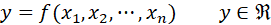
と表せるかもしれません。各保険会社の商品や特性、経済環境などの様々な要素をインプットし、同じ尺度で評価し、各保険会社の健全性の大小を一次元で表すものだと思います。

簡便計算のためには、この関数の性質を理解する必要がありますが、まずは、部分的な理解（例えば、分子や適格資本、分母のリスク量、別々での理解）から始めるということが可能だと思います。

関数で表したため、何が言いたいか分かりづらくなってしまったら申し訳ありません。

１つの例を挙げたいと思います。先ほど、SMRのファクター方式というものを挙げました。これは、上記の過去問の模範解答に基づくと、「エクスポージャー等の基準額に所定のファクターを乗じて、リスク量を算出するモデル」ということになります。つまり、関数で表すと、

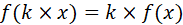
と表せるものと思います。ここで、はリスク量を表す関数で、が基準額、がファクターということになります。

ESRの計算において、信用リスク等の計算は、このファクター方式となっています。

ファクター方式というのは線形的な性質があると言い換えることもできます。つまりエクスポージャーが増加すれば比例してリスク量も増加すると意味です。分かりやすい性質だと思います。

ファクター方式でないものの例として大量解約リスクがあります。これは、私見になりますが、大量解約リスクも線形的な性質を持っていると考えています。大量解約リスクの計算では、初年度にショック（日本の場合は30%）が発生し、それ以降のキャッシュフローが３割減となります。これは、エクスポージャーである純資産が約３割減少することになるため、大量解約リスクは、純資産の約30%と表せるのではないかと考えています。ここで、「約」をつけているのは、線形性を与えない性質もあるためであり、例えば、解約控除がある場合はその分は一時的に純資産の増加に貢献します。

全てのESRの計算のための要素がシンプルに表現できれば苦労しませんが、実際はそうではありません。

では、簡便計算を実現するために、具体的にどのように理解を深めるのかについては、今のところ正解を持ち合わせていません。ひとつの方法としては、感応度分析や変動要因分析などを分析を重ねて、経験やノウハウを蓄積する方法があると思います。

上記の対話の例では、精緻に計算することを挙げましたが、その場合でも計算されたESRが妥当かどうか分析や検証をするでしょう。なぜESRが変わったのか経営陣に説明できるように準備する必要があるためです。ただ、そこで終わってほしくはなくて、そのような経験を経て、ESRの特性を知り、こういう性質があるのではないか、というまで深堀していくことが重要だと思います。

また、計算して得た結果を見て、それなりに妥当な説明を考えるのは慣れてくればできますが、それ以上に、計算せずに結果を予測し、実際に計算してみてズレがあった場合はなぜ違ったのか、という思考をめぐらせてブラッシュアップしていくことも重要だと思います。

場合によっては、さらに理解が深まり、例えば、「ESRにはこういう性質があるが本当に実態を表しているのか」といった気づきを得ることがあるかもしれません。そういう発見をできれば、将来、有識者として保険業界に貢献できる人材になれる可能性があるのではないかと思います。

今回お話したことは、ESRに限らず、専門性のあるアクチュアリー職としては重要なことだと思っています。アクチュアリー業界の発展のため、個々のアクチュアリーが成長することを願っております。

（ペンネーム　緑黄色野菜）