2018年12月14日（金）のコラム（アクチュアリー試験講評（2018年度 生保数理 編））で、今年度のアクチュアリー試験（生保数理）の講評を行いましたが、特に、問題3（2）については、その後、気付いた点が幾つか出てきました。

そこで、今回のコラムでは、講評の補足として、『過去法の責任準備金』に焦点を当てて、気付いた点を列挙してみますので、受験生の一助となれば幸いです。
　

１．責任準備金を求める５つのテクニック

　頻出パターンである『保険料年払全期払込、死亡保険金期末払の養老保険』の責任準備金を求める主なテクニックは、以下の５つに分類されます。
（１）重要公式 \(_tV_{x:\overline{\ n\ |}}=1-\frac{\ddot{a}_{x+t:\overline{\ n-t\ |}}}{\ddot{a}_x:\overline{\ n\ |}}\ \ (0 \leq t \leq n)\)
（２）責任準備金の再帰式
（３）将来法
（４）Thiele（ティーレ）の微分方程式
（５）過去法
　上記のテクニックは、ほぼ出題頻度の順番に並んでいますので、特に、生保数理をこれから勉強される方は、上記の順番で勉強を進めると良いでしょう。

２．過去法を用いる問題の見極めテクニック

　１．で列挙したテクニックのうち、Thiele（ティーレ）の微分方程式は、３つの条件（保険料が一時払、死亡保険金が即時払、死亡保険金が責任準備金比例）が成立する場合に利用できます。この３つの条件が問題文に与えられていれば、このテクニックを用いると見極めできます。
　さらに、過去法についても、問題文に、２つの条件（\({\large \begin{smallmatrix} 1 & \, & 1 \\ x & , & \overline{\ n\ |} \end{smallmatrix}}\) ）、つまり、加入年齢xの上に１があり、かつ、保険期間（nなど）の上に１があるような条件が与えられれば、過去法の責任準備金を用いると見極めできます。その際、教科書（上巻）183ページ問題（3）（4）の公式を利用すれば早く解けます。
　もちろん、2018年度（生保数理）問題3（2）のように、問題文に『過去法により平準純保険料式責任準備金を導出』というようなあれば、過去法を用いるしかありませんが。

３．過去法は、『過去から現在に向かって』なのか？『過去の期間で』なのか？

　教科書（上巻）177ページの3～4行目の式をみれば、過去法とは、『過去から現在に向かって』計算する、つまり、『終価』を考えることとなります。ところが、同ページの（5.3.1）をみると、分子が、加入からt年経過までの『過去の期間で』計算されていることがお分かりいただけると思います。
　一方で、責任準備金の計算時点は、あくまでも到達年齢『x+t歳』となります。実際、同ページの（5.3.1）をみると、分母が（加入年齢『x歳』ではなく）到達年齢『x+t歳』となっています。
　つまり、将来法か過去法かの違いは、『分母』の添え字が加入年齢か到達年齢かという違いであるとも言えます。もちろん、将来法と比較して、収入と支出の順序が逆、つまり、『収入終価』から『支出終価』を引いたものです。
　なお、確定年金の公式（例．教科書（上巻）16ページ（1.6.1）～（1.6.4）など）をご覧いただければ、確定年金のける現価と終価の違いは、『分子』にあることに気付くと思います。したがって、現価と終価の違いを表示する『場所』が『分子』か『分母』かという点は、確定年金と生命年金の違いの一つと言えそうです。

４．2018年度（生保数理）問題3（2）の条件（Ⅰ）

　2018年12月14日（金）のコラムで示したとおり、本問は、教科書（上巻）201ページ問題（7）の類題ですが、それよりも、昭和45年度（保険数学Ⅰ）問題６の類題（というか同じ問題！）と言うべきかもしれません。
　しかし、両者の問題を比較した場合、ある前提が異なる点に気付かれると思います。それは、初年度末責任準備金が正値かどうかという点です。実際、2018年度（生保数理）問題3（2）では、『初年度末責任準備金が正値』という前提がないため、条件（Ⅰ）が成立しても、以下のような『反例』が見つかります。

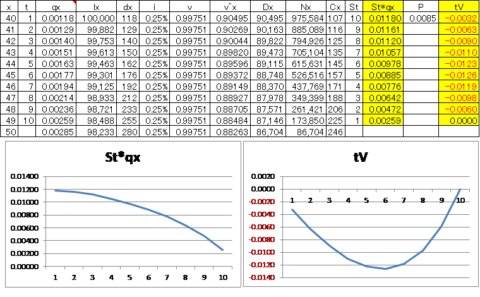
　特に、穴埋め問題の ⑤ について、条件（Ⅰ）のみから一意に決まるように問題文が読めるのですが、より厳密には、条件（Ⅰ）かつ選択肢から、⑤ が一意に決まるようにも思えます。
　いずれにせよ、アクチュアリー会から公表される公式解答（昨年は3月末頃に同会ホームページで公表）が待ち遠しいですね。

５．平成27年度（年金数理人会試験）基礎数理Ⅱ問題1（2）

　過去法に関連して、平成27年度（年金数理人会試験）基礎数理Ⅱ問題1（2）では、連続払確定年金の責任準備金（保険料積立金）が最大となる経過年数を求める問題ですが、高校の数学で学んだ、微分係数がゼロ、つまり、極値を求める問題に帰着
　また、本問の場合、アクチュアリーの大先輩である、山内正憲氏が執筆された、『保険数学（森北出版）』

の214ページにある『前観法』、『後観法』の公式を用いれば、比較的簡単に解けます。なお、『前観法』、『後観法』は、生保数理の教科書に登場する『将来法』、『過去法』に対応するもので、具体的には、以下の公式となります。

前観法　⇒　\(_{t}\overline{V} = \frac{1}{_{t}p_x v^t}[{\int_o^t} _{t}p_x v^t (\overline{P}_{t} – u_{x+t} U_{t}) dt]\)
後観法　⇒　\(_{t}\overline{V} = \frac{1}{_{t}p_x v^t}[{\int_t^n} _{t}p_x v^t (u_{x+t} U_{t} – \overline{P}_{t}) dt + _{n}p_x v^n T]\)

　いかがでしたか。この機会に、是非、過去法の責任準備金に慣れ親しんでいただければ幸甚に存じます。（ペンネーム：活用算方）